משפט התיכון

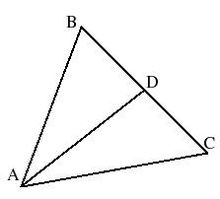
AD תיכון ל-BC

השטח הירוק ועוד השטח הכחול שווה לשטח האדום

בגאומטריית המישור, משפט התיכון קובע שסכום ריבועי שתי צלעות במשולש, שווה לסכום מחצית ריבוע הצלע השלישית, ופעמיים ריבוע התיכון לה.

כלומר, אם במשולש ABC הנקודה D היא אמצע BC, מתקיים: $AB^{2}+AC^{2}=2AD^{2}+{\frac {BC^{2}}{2}}$

משפט התיכון הוא מקרה פרטי של משפט אפולוניוס הקובע: אם במשולש ABC הנקודה D נמצאת על BC ומחלקת אותו ביחס n:m (כלומר mBD = nDC), מתקיים:

$\ mAB^{2}+nAC^{2}=mBD^{2}+nDC^{2}+(m+n)AD^{2}$

במקרה של משפט התיכון, הנקודה D מחלקת את BC ביחס של 1:1.

הוכחה

נסמן את היטל AB על BC ב-p (אם $\angle ABC>{\frac {\pi }{2}}$ אז p<0)

במשולש ABC, נקבל, על פי משפט הקוסינוסים: $AC^{2}=AB^{2}+BC^{2}-2p\cdot BC$

נעביר אגפים, ונקבל: $2p\cdot BC=AB^{2}+BC^{2}-AC^{2}$

במשולש ABD, נקבל, על פי משפט הקוסינוסים: $AD^{2}=AB^{2}+BD^{2}-2p\cdot BD$

נציב $BD={\frac {BC}{2}}$, ונקבל: $AD^{2}=AB^{2}+{\frac {BC^{2}}{4}}-p\cdot BC$

נעביר אגפים ונכפיל ב-2, ונקבל: $2p\cdot BC=2AB^{2}+{\frac {BC^{2}}{2}}-2AD^{2}$

על פי כלל המעבר, נקבל: $AB^{2}+BC^{2}-AC^{2}=2AB^{2}+{\frac {BC^{2}}{2}}-2AD^{2}$

לאחר העברת אגפים, נקבל: $2AD^{2}+{\frac {BC^{2}}{2}}=AB^{2}+AC^{2}$

הוכחה גאומטרית

נסמן $AB=a,AC=b,BC=c$. כמו כן נסמן $AD=x$

אם $a=b$, המשולש שווה-שוקיים והתוצאה מתקבלת מידית מהפעלת משפט פיתגורס.

אחרת, $a\neq b$, נחשב את שטח המשולש $\Delta ABD$ לפי נוסחת הרון:

$S_{\Delta ABD}={\sqrt {{\Bigl (}{\frac {x+a+{\frac {c}{2}}}{2}}{\Bigl )}\cdot {\Bigl (}{\frac {x+a+{\frac {c}{2}}}{2}}-x{\Bigl )}\cdot {\Bigl (}{\frac {x+a+{\frac {c}{2}}}{2}}-a{\Bigl )}\cdot {\Bigl (}{\frac {x+a+{\frac {c}{2}}}{2}}-{\frac {c}{2}}{\Bigl )}}}=$

${\sqrt {{\Bigl (}{\frac {(a+{\frac {c}{2}})+x}{2}}{\Bigl )}\cdot {\Bigl (}{\frac {(a+{\frac {c}{2}})-x}{2}}{\Bigl )}\cdot {\Bigl (}{\frac {x-(a-{\frac {c}{2}})}{2}}{\Bigl )}\cdot {\Bigl (}{\frac {x+(a-{\frac {c}{2}})}{2}}{\Bigl )}}}=$

${\frac {1}{4}}\cdot {\sqrt {{\Bigl (}(a+{\frac {c}{2}})^{2}-x^{2}{\Bigl )}\cdot {\Bigl (}x^{2}-(a-{\frac {c}{2}})^{2}{\Bigl )}}}={\frac {1}{4}}\cdot {\sqrt {-x^{4}+x^{2}\cdot {\Bigl (}2a^{2}+{\frac {c^{2}}{2}}{\Bigl )}-{\Bigl (}a^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}}}$

נחשב את שטח המשולש $\Delta ACD$ ונקבל באותו אופן את התוצאה הבאה:

$S_{\Delta ACD}={\frac {1}{4}}\cdot {\sqrt {-x^{4}+x^{2}\cdot {\Bigl (}2b^{2}+{\frac {c^{2}}{2}}{\Bigl )}-{\Bigl (}b^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}}}$

התיכון מחלק את המשולש לשני משולשים שווי שטח, כלומר $S_{\Delta ABD}=S_{\Delta ACD}$. נשווה ביניהם ונמצא את $x$

${\frac {1}{4}}\cdot {\sqrt {-x^{4}+x^{2}\cdot {\Bigl (}2a^{2}+{\frac {c^{2}}{2}}{\Bigl )}-{\Bigl (}a^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}}}={\frac {1}{4}}\cdot {\sqrt {-x^{4}+x^{2}\cdot {\Bigl (}2b^{2}+{\frac {c^{2}}{2}}{\Bigl )}-{\Bigl (}b^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}}}$

נכפיל פי 4 ונעלה את שני האגפים בריבוע:

$-x^{4}+x^{2}\cdot {\Bigl (}2a^{2}+{\frac {c^{2}}{2}}{\Bigl )}-{\Bigl (}a^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}=-x^{4}+x^{2}\cdot {\Bigl (}2b^{2}+{\frac {c^{2}}{2}}{\Bigl )}-{\Bigl (}b^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}$

נסדר את המשוואה:

$x^{2}\cdot {\Bigl (}2a^{2}+{\frac {c^{2}}{2}}-2b^{2}-{\frac {c^{2}}{2}}{\Bigl )}={\Bigl (}a^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}-{\Bigl (}b^{2}-{\frac {c^{2}}{4}}{\Bigl )}^{2}$

$2(a^{2}-b^{2})x^{2}={\Bigl (}a^{2}-{\frac {c^{2}}{4}}-(b^{2}-{\frac {c^{2}}{4}}){\Bigl )}\cdot {\Bigl (}a^{2}-{\frac {c^{2}}{4}}+(b^{2}-{\frac {c^{2}}{4}}){\Bigl )}$

$2(a^{2}-b^{2})x^{2}=(a^{2}-b^{2})\cdot {\Bigl (}a^{2}+b^{2}-{\frac {c^{2}}{2}}{\Bigl )}$

נצמצם ב $a^{2}-b^{2}$ (זו פעולה חוקית מכיוון שהנחנו כי $a\neq b$) ונקבל את התוצאה: $2x^{2}=a^{2}+b^{2}-{\frac {c^{2}}{2}}$